Análisis de datos#
El análisis de datos de NovaLabUD está orientado a la visualización de datos, la limpieza, transformación y la modelización estadística. Esta sección tiene como fin mostrar los análisis estadísticos y generar informes visuales usando el software. No es necesario tener conocimientos previos de programación, pero se recomienda familiaridad con conceptos básicos de estadística.
Selección de Variables Independientes y Dependientes#
Después de haber cargado los datos en el programa, para realizar un análisis de regresión o interpolación, es necesario definir qué variables serán consideradas independientes (predictoras) y cuáles serán las dependientes (a predecir). Se selecciona la variable independiente que el usuario considere, influencia a otras variables en el conjunto de datos (Variable X), y la variable independiente (Variable Y) como se muestra en la figura Selección de variables.. Esta ventana emergente aparece cada vez que se seleccione algunos de los ajustes de regresión o interpolación, estas opciones se despliegan al seleccionar el botón de Edición (ver figura Regresiones disponibles para el ajuste de datos.).
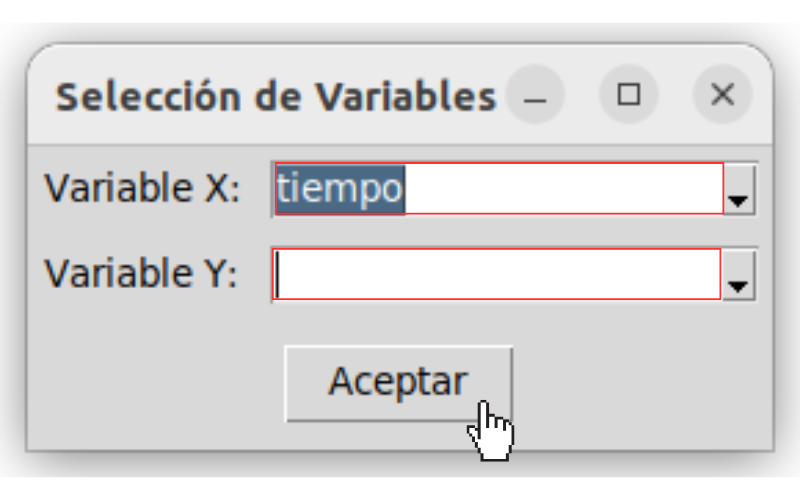
Selección de variables.#
El software permite que el usuario digite el nombre de la columna en el campo correspondiente o en su defecto usar la lista desplegable que contiene todas las columnas del conjunto de datos, lo que facilitará la selección de las variables.
Tipos de Análisis y Ajustes Disponibles#
Una vez se hayan seleccionado las variables a utilizar, el siguiente paso es elegir el tipo de análisis que se desea realizar. NovaLabUD permite realizar tres tipos de análisis: regresión lineal, regresión polinómica e interpolación. Este menú desplegable se puede localizar seleccionando el botón Edición y posteriormente Regresiones.
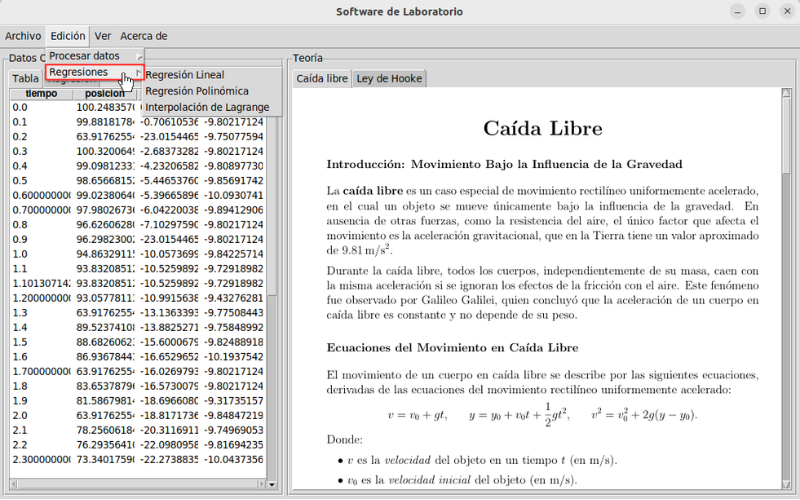
Regresiones disponibles para el ajuste de datos.#
Regresión Lineal#
La regresión lineal es una técnica utilizada para modelar la relación entre una variable dependiente y una o más variables independientes. El modelo asume que la relación entre las variables es lineal.
Cómo Funciona: El software ajustará una línea recta a los datos seleccionados, buscando minimizar el error cuadrático medio.
Selección: Seleccionar Regresión Lineal como el modelo deseado en el menú desplegable mostrado en la figura anterior.
Regresión Polinómica#
Si los datos muestran una relación no lineal, la regresión polinómica puede ser más adecuada. Este modelo ajusta una curva polinómica de grado N al conjunto de datos.
Cómo Funciona: El software ajustará un polinomio de grado 2, 3, o superior, según lo que el usuario seleccione (ver figura Selección grado del polinomio.).
Selección: Se selecciona Regresión Polinómica y se especifica el grado del polinomio en la ventana emergente (por ejemplo, 2 para cuadrática, 3 para cúbica).
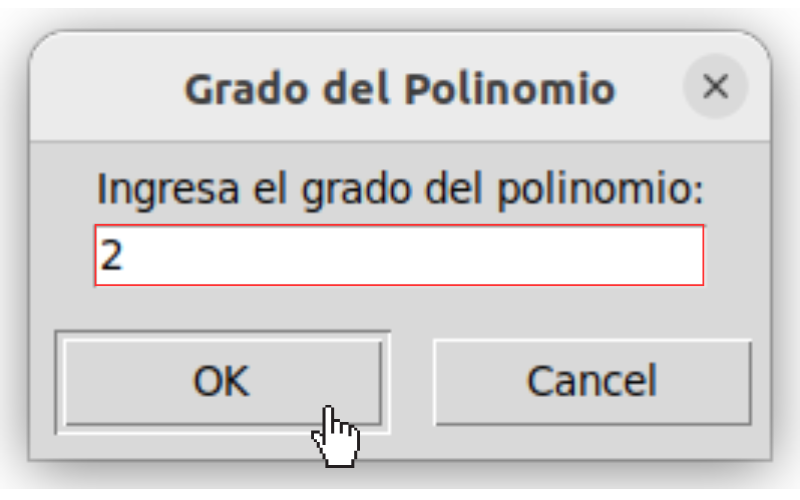
Selección grado del polinomio.#
Interpolación#
La interpolación se utiliza para estimar valores dentro del rango de un conjunto de datos existente. Este ajuste es útil cuando se desea predecir valores en puntos específicos basados en los datos disponibles.
Cómo Funciona: El software ajustará el modelo de interpolación proporcionando predicciones en los puntos deseados. Al igual que en el modelo anterior aparecerá una ventana emergente solicitando el grado del polinomio para proceder con el ajuste.
Selección: Seleccionar Interpolación como el modelo deseado para ajustar los datos.
Generación Automática de Gráficas#
Una vez que se haya completado el ajuste, NovaLabUD generará automáticamente una gráfica visualizando el modelo ajustado junto con los datos previamente tratados. Esto permitirá inspeccionar visualmente la calidad del ajuste.
La gráfica de dispersión mostrará los puntos de datos originales (variables dependientes vs. independientes).
La curva de ajuste (ya sea recta en el caso de la regresión lineal, o curva en el caso de la regresión polinómica o interpolación) se dibujará sobre los puntos de datos.
Esta gráfica automática se puede visualizar en el panel izquierdo de la ventana principal simplemente seleccionando la pestaña de Regresiones, tal como se muestra a continuación.
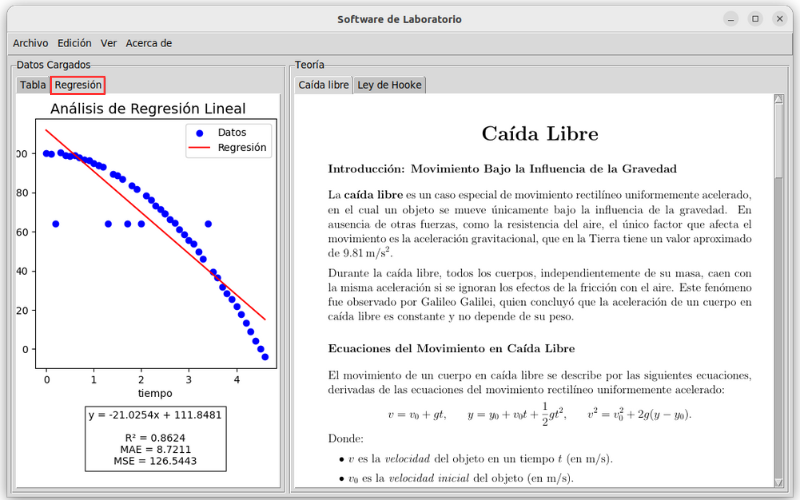
Visualización del modelo Regresión Lineal.#
Cálculo de Métricas de Evaluación del Ajuste#
Después de seleccionar el tipo de análisis y ajustar el modelo, la aplicación calculará varias métricas que permitirán que el usuario evalúe la calidad del ajuste. Las métricas que NovaLabUD permite calcular son:
\(R^2\) Coeficiente de Determinación#
El \(R^2\) es una métrica que indica la proporción de la varianza de la variable dependiente que es explicada por las variables independientes en el modelo. Un valor de \(R^2\) cercano a 1 indica un buen ajuste del modelo a los datos.
MAE (Error Absoluto Medio)#
El MAE mide el error promedio entre los valores predichos por el modelo y los valores reales. Cuanto más bajo sea el MAE, mejor será el ajuste.
MSE (Error Cuadrático Medio)#
El MSE calcula el promedio de los errores al cuadrado entre las predicciones y los valores reales. Al igual que el MAE, un MSE más bajo indica un mejor ajuste.
SE (Error Estándar)#
El SE mide la precisión de las estimaciones del modelo, proporcionando una idea de la dispersión de los errores.
Estas métricas se pueden visualizar debajo de la gráfica donde se muestran los datos y el modelo de ajuste. Además, se puede visualizar la ecuación del gráfico.
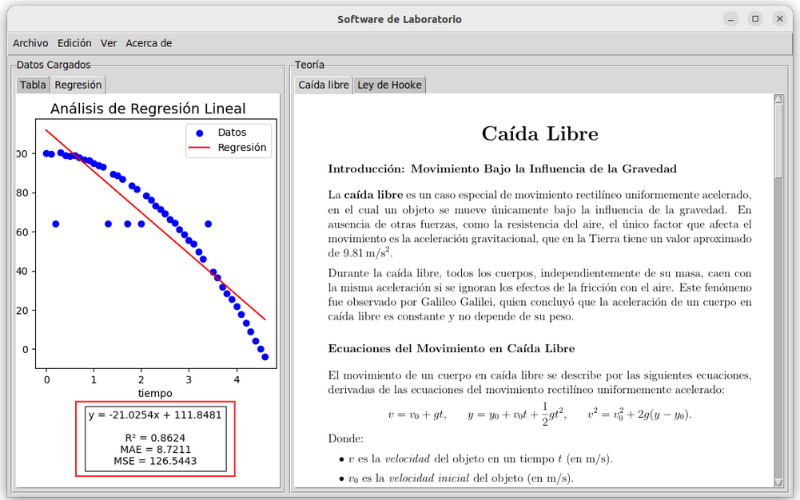
Métricas de evaluación para un ajuste por Regresión Lineal.#
Interpretación de los Resultados#
Después de haber calculado las métricas de calidad y generada la gráfica, es fundamental interpretar adecuadamente los resultados:
Si el valor de \(R^2\) es cercano a 1, esto sugiere que el modelo explica bien la variabilidad de los datos.
Si el MAE y MSE son bajos, el modelo ha ajustado bien los datos y tiene un buen poder predictivo.
La gráfica permite observar si el modelo es adecuado. Si los puntos de datos se agrupan cerca de la línea o curva ajustada, esto indica un buen ajuste.
